第1回 なぜ、「ヤマ」のある線分図で教えるのか。 ～和差算の線分図は、１次方程式を解くための道具だった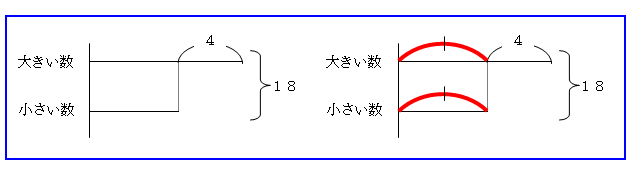～  第1回目の今回は、中学受験の算数と切っても切れない縁にある線分図について、「なぜ、『ヤマ』のある線分図で教えるのか」というテーマを、和差算の指導を通してお話ししていきたいと思います。 線分図といっても、ここでは、主に「和差算」、「分配算」「倍数算」などに使う線分図のことを主に取り上げていきます。速さ問題の「はじきの線分図」や「年齢算の線分図」については、別の機会にお話させていただきます。 １－１．和差算とは 線分図の考え方をご説明する前に、和差算とは何かをご説明します。和差算の「和」とはたし算の答えのこと、「差」とは引き算の答えのことです。２つの数があり、大きい数と小さい数をたした答えと、大きい数から小さい数を引いた答えがわかっているとき、これらの答え、つまり「和」と「差」を使ってもとの２つの数を求めるような問題を「和差算」といいます。もちろん、３つ以上の数を扱った問題も数多くありますが、使い方・考え方は変わらないので、はじめは２数で説明していきます。 １－２．和差算の線分図 「和差算」の文章題を解くときに活躍するのが「線分図」といわれるものです。「大小２つの数」を線の長さで表すことにして、その長さの和や差から、それぞれの数を求めます。まず、一般的な書き方を簡単な問題で説明していきます。 １－３．線分図の書き方の手順
① 「大きい数」「小さい数」と、まず左側に書きます。 ② それぞれの線の書き出し位置をそろえるために、適当な長さの縦線をひきます。 ③ 大きい数の線の長さを小さい数より少し長くします。 ④ 線の長い分が２つ数の差ですから、長い分の線の上か下に「４」と書きます。 ⑤ また、右側に２つの数の行にまたがるようにカッコを書き、和の「18」を書き込みます。 【基本の図】 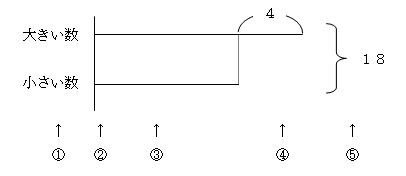 これで基本の図は完成です。 さらに進化させ、「ヤマ」を書かせると、教えやすく、わかりやすい。 １－４．「ヤマ」を書いて、解法時のターゲットを明確に。 基本の図に、さらに「ヤマ」を書き加えておくと指導がしやすくなります。 「ヤマ」とよんでいるのは、小さい数の線分を両端とした「弧（図の赤部分）」のことです。 【ヤマのある図】 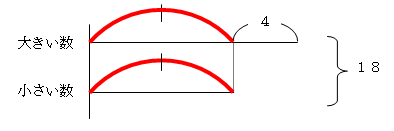 この部分を「ヤマ１個」とすると、大きい数は「ヤマ１個」たす「４」となります。この「ヤマ１個」の値を求めれば答えが出ます。基本の前図と比べると、問題を解く際のターゲットがはっきりしたのがわかりますね。 今後、さまざまな問題でこの「ヤマ」に活躍してもらうことになりますので、面倒でもこの「ヤマ」を書くクセをつけさせておきましょう。 １－５．実際の授業では・・・ （線分図を書くまで） 先生：「求めたいものは、ここでは、大小２つの数ですが、小さい数を「ヤマ１個」としてください。これと同じヤマを、大きい数にも書き込み、４大きい分だけ長くします。 大きい数は、「ヤマ１個」たす「４」、小さい数は、「ヤマ１個」となりました。この「ヤマ１個」の値がわかれば、大きい数も小さい数もわかりますね。 （解き方の指導） 先生：「ヤマ」以外でじゃまなのは、「４」です。「４」がなければ、「ヤマ」だけの図になる訳ですから、まず、この「４」をとってしまいます。２つをたして18だったのですから、右の18からも４をとってしまいます。18－４＝14で、２つの和は14になりますね。これを右側の「和」を表すところに書き込みます。 これで、ヤマ２個分が14とわかったので、ヤマ1個分は14÷２で７となります。 この「７」をそれぞれのヤマのところに書き込みます。小さい数はヤマ１個分なので、７。大きい数はヤマ１個分たす４ですから、７＋４で11となります。 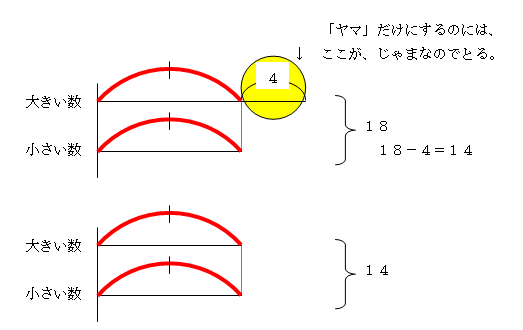 ヤマ２個＝１４ ヤマ１個＝１４÷２ ヤマ１個＝７ １－６．「ヤマを１個」を「ｘ」に変えると、１次方程式になる。 授業での指導方法を読んで、もう気づいた方もいらっしゃるでしょう。「ヤマ」は「ｘ」の代わりだったのです。これが、どうしても「ヤマ」が必要だった理由です。これがないと、１次方程式の式をつくるとき際の「ｘ」に該当するものが不明なままで説明することになるからです。 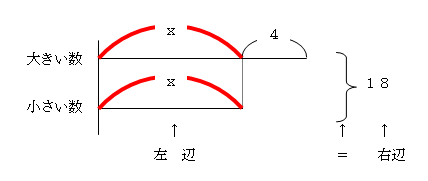 １次方程式による解法： 小さい数をχとすると、大きい数はｘ＋４となる。 ｘ＋（ｘ＋４）＝18 ２ｘ＋４＝18 両辺から４を引いて ２ｘ＝14 エックス１個分を求めればよいのだから、 両辺を２で割って ｘ＝７ 和差算の線分図による解き方は、実は「等式」を視覚的に理解しやすくした「線分図」という形であらわし、さらに「等式の性質」を使った方程式の解法まで身につく非常に優れたものだったのです。 １－７．ご家庭では、「ヤマ」を書いて考えるクセをつけさせてください。 「ヤマ１個」の書き込みで和差算解法の見晴らしがよくなったように、ちょっとした気づかいで子どもたちは「よくわかる」ようになるものです。「和差算」「分配算」「倍数算」など、必ず「ヤマ」を書かせるクセをつけさせてください。「ヤマ」は「ｘ」の代わりです。中学、高校の数学にも直結する等式の性質を利用して方程式を解くという考え方が、必ず身につくようになります。 では、第1回目はここまでで。 [PR]Samurai Sounds
 仲麿ゼミナールへ戻るソフト販売Nakamaroへ戻る |
第2回 文章で書いて身につく「つるかめ算」＞＞